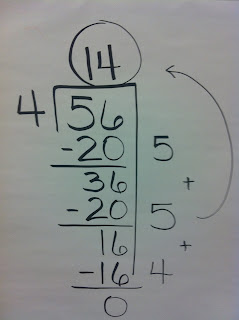Magnet Explorations

Our first day exploring with magnets proved to be quite interesting. In addition to having some fun, we also brought out a lot of our prior knowledge about magnets and their properties, which the students learned back in 2nd Grade.

*All magnets have invisible magnetic fields.
*Some magnets are stronger than others.
*Magnets come in different shapes and sizes.
*The Earth is like a giant magnet.
*Magnetism is a force (push/pull).
*All magnets have a North and a South Pole.
*Like poles repel (or push away from each other).
*Opposite poles attract (or pull toward each other).

Upcoming investigations will explore what happens to a magnet's poles when the magnet is broken. We will also make a temporary magnet and test its varying strength when it is magnetized to different levels of strength. After participating in a Gizmo virtual lab on magnetism, students will design and create their own magnet experiments by formulating and exploring their own "testable questions".

Enjoy our slideshow. :-)
Explorations with Magnets on PhotoPeach

Variables

Variables on PhotoPeach

In studying agents of weathering & erosion in recent weeks, our classes have learned to identify variables in scientific investigations. By the way, we think hands-on science is REALLY COOL!

Controlled Variables- also known as “Controls”
These are set-ups that remain in their original condition as we participate in an investigation, so that after a lab, we can look back at them and compare our end results with what the original, “un-touched” condition was like.

Untouched “sugar cube”, “cookie”, and “sand tray”

Independent Variables- also referred to as what “I” did (“I”ndependent)
This refers to what "we" as the experimenters change as we progress through a lab.

We changed from slow to vigorous shaking to see the effects of “wind” weathering on “rocks” (sugar cubes).

We changed from 5 squirts, to 10 squirts, to 15 squirts to see “water” weathering on earth (cookies).

We changed from "no wind breaker" (barrier) to adding a wind breaker in order to see how people work to prevent “wind” erosion.


“D”ependent Variables- also referred to as the (“D”ata)

This refers to what changed or happened in the experiment as a result of the Independent Variable (what "I" did).

*The vigorously shaken cubes were more weathered than the gently shaked cubes.
*The more saturated cookies were more weathered than the less saturated cookies.
*The wind breakers stopped the wind from eroding and hitting the “building” at the end of the tray.

For Behavior Bucks, leave a comment on what the independent and dependent variable would be in the following experiment:

Carter's Plant Experiment.....

Carter wants to test the effects of plant growth with and without sunlight. He buys two identical plants at the hardware store. He puts "Plant A" in a dark closet and "Plant B" in front of a window to receive sunlight. Each day he checks his plants and records data on what he observes. He also carefully waters each plant the same amount of water once each week. After three weeks, Carter finds that Plant B grows better because it receives sunlight.

What was the independent variable in this experiment?
What was the dependent variable in this experiment?
Be sure to leave your first name at the end of your comment!

Divide and Conquer

In Math Workshop, we have been working to connect division to multiplication. Many times, we even find ourselves thinking of division problems as multiplication problems so that we can use a multiplication strategy to solve them.
Consider 56 divided by 4

When looking at this division problem, we ask ourselves, “How many 4’s are in 56?”. By doing this, we recognize that we will be finding the number of groups of 4 that are in 56, or _____ x 4 = 56.

Many students then find it simple to use an efficient form of Skip-Counting by multiples of 4 to determine the answer. Starting with the 10th multiple of 4 would be very common. The answer is 14. It takes 14 groups of 4 to equal 56.

Other students would incorporate this same strategy into a different model, such as a Multiplication Cluster. The approach uses decomposition of one of the factors to make smaller, easier probloems. In the example below, again 14 is decomposed into 10 and 4 to make the two easier problems. 10 groups of 4 is 40. Adding another 4 groups of 4 (4x4) or 16 “builds” 14 x 4 = 56. 56 divided by 4 can also be thought of as 56 divided by 2, and again divided by 2 (dividing by 2 twice is the same as dividing by 4). Some students like to refer to this strategy as the “Halfsie-Halfsie”. 56 divided by 2 is 28. 28 divided by 2 is 14. This strategy only works when 4 is the divisor.

A more advanced strategy would be to take the dividend (total) and decompose it into smaller multiples of the divisor to make smaller division problems that would “build “ (add up to) the original division problem. This method is called a Division Cluster. 56 could be decomposed into 20 + 20 + 16 and solved as three smaller division problems. 20 divided by 4 is 5. 20 divided by 4 is 5. 16 divided by 4 is 4. 56 divided by 4 is 14.

Last but not least, the Partial Quotients Method (also lovingly referred to as the “Russian Peasant” Method), is a special model we move our students toward in order to progress their thinking into a more “standard algorithmic” set-up. If you look carefully at the smaller problems that are solved in each of the examples shown below, you will see that they are the same as in the earlier examples. Even though the mathematical “models” are different, the “strategy” of using good mathematical sense to decompose the dividend into smaller numbers (landmark multiples of ten or single digit numbers) is the same, so that the reasonableness of solutions can be easily assessed (Does my answer make sense?).

Our approach is a conceptual-based approach, teaching students that there is a relationship between multiplication and division and there is a meaning as to the dividend, divisor, and quotient. One represents the total (dividend) and the other two parts represent the number of groups and the size of the groups that make up the total.

Promoting this deep understanding at Grade 4 will then more easily transfer later (5th Grade) into understanding why the division algorithm works (which is very abstract in nature and cumbersome to understand conceptually).

Happy Dividing!

P.S.- Students, leave a comment sharing your favorite divison strategy (and why), and earn Behavior Bucks to spend at your next class auction!

What Can I Do to Help?

You might be wondering, as we approach the end of the first nine weeks, what you can do to help your reader do better.  While Mrs. Montero and Mrs. Nash are really excited and proud to see improvements in many young readers already, we know 4th grade reading can be HARD.

Here are some things you can do to help your child on their reading comprehension tests.

1.  Each time a grade comprehension test comes home, help them to revise every item they missed, even if they earned an A!  Some of our most powerful learning in life comes from our mistakes, and reading comprehension tests are no different.  When revising, read through the entire passage with your child first.  Then, discuss ALL of the answer choices and how we know they are right or wrong.  Constantly refer back to the clues in the text, knowing that some clues are clearly stated and others are scattered throughout the text.

2.  Ensure that your child is reading for 20 minutes or more each night.  No, we are not telling you to get out the timer and start counting pages and minutes again.  We are reminding you that reading is the single most powerful practice available.  Research and experience tells us that readers who really and truly are reading every single day (Yes, that means weekends, too.) are more successful in all areas of learning.  Think of daily reading as a daily multivitamin for their school success.  It is critical.

3.  Schedule time throughout the week and weekend for your child to use FCAT Explorer.  This tool has been available to Florida students for years.  It is aligned to the same standards assessed on these classroom reading comprehension tests, as well as the FCAT.

4.  Make sure your child is in class daily.  The instructional strategies we use at Chets Creek cannot be duplicated with a worksheet at home.  When children miss school, they are missing out on learning.  We try to "catch them up" as best we can, but it is never quite the same.

5.  Start a "Mommy and Me" or "Daddy and Me" book club and read WITH your child.  Often we think that because our readers are old enough to read independently and in their heads, we don't need to read with them anymore.  However, reading shared with an adult is not just independent practice anymore, but an opportunity to learn new ways of thinking about their reading.  In addition to being a powerful family experience, sharing a book with your child allows you to talk with them about the book, giving them a window into the mind of an adult reader.  Having the support of a "leader reader" also allows your child to climb inside a story or text that might have been too difficult for them on their own.  When you hear a tiny thought in your head saying, "Oh, he's going to ....." or "Why did she do that?", speak these thoughts aloud to your child and open a discussion.  Talk about what the author wrote that sparked those thoughts in your mind.

With busy schedules, it might not be realistic to say you will sit down and read with them every single night.  But perhaps you choose a book to share and read it every other night, two days a week, or on the weekends.  The other days, your young reader can read their own independent book.

Decomposing an Array

One of the ways to view multiplication is to consider the area of an array. The dimensions of the array are the factors and the area is the product. Using array cards, students work on their basic facts. Array cards not only help with fluency, but students also begin to understand that the shape of the array is an indicator of how far the factors are "apart". A square array indicates a square number (both factors are the same)and a long and skinny array indicates factors that are very different in magnitude.
One of the strategies we use to solve multiplication problems with larger factors is decomposing. To model this strategy, we use generic arrays. An example of a generic array is pictured below.


A generic array can be decomposed by drawing either a horizontal or vertical line through the array. In doing so, one of the two factors is broken into two smaller numbers which add to the original dimension. In the first example, 12 is decomposed into 10 and 2. The idea is to create two smaller problems that are much easier to solve. 15 x 10 and 15 x 2 are much easier to solve than 15 x 12. Decomposing the large array into multiples of 10, 5, and 2 seem to be the easiest. Once the two smaller areas (products)are found, they are recomposed to find the area (product) of the large array. In our example: 15 x 10 = 150 and 15 x 2 = 30, so 15 x 12 = 150 + 30 = 180.

Fourth Grade Writes Night

Fourth Grade Writes Night was a success!  The students shined while demonstrating a Writer's Workshop lesson on how to revise a story.  Parents and students went home with a packet of information about what to do in class and at home to become better writers.  Thanks to all the families who came out to learn more about the FCAT Writing expectations.

Unexpected Outcomes

At Chets Creek, we work towards creating a high quality student that will become a lifelong leader.  We want our learners to be community contributors, collaborative workers, complex thinkers, quality producers, effective communicators, and self-directed learners.

Last week, a few of Mrs. Nash's readers took a risk in order to contribute to their classroom and school community.  These two girls ran with their creative idea to set up a lemonade stand in their neighborhood to raise money to help fund our Nook project.  They raised about $14, which is only a fraction of the money we need.  But, these girls understand that if we all raised $14....well, I'll let you figure that out, dear mathematician-readers.  If 41 students raised $14 each, how much money would we raise to put towards our Nook project?


Thanks, girls, for being self-directed, community contributors.